Design of Composite Slab-Bondek II


Properties of Bondek II
Type Data   Reference
Cover width   mm    
Depth of decking hp = mm  
Pitch of deck ribs   mm  
Crest width   mm  
Design sheet thickness   mm  
Deck weight gp= kN/m2  
Yield strength   N/mm2  
Characteristic yield strength fyk,p = N/mm2  
Design thickness tp = mm2/m  
Effective area of cross-section Ap = mm  
Height to neutral axis e = mm  
Second moment of area of steel core Ip = mm4/m  
Plastic moment of resistance kNm/m   This number will be used in checking longitudinal shear using partial-interaction method.
Characteristic resistance to vertical shear kN/m Assumed  
Characteristic resistance to horizontal shear N/mm2 Assumed  
For re-entrant profiles, the minimum width should be used. b0 = mm    
           


Input Data of Composite Slab-Bondek II
Type Data Check Reference
Floor plan data  
  Span of slab L L= m   (full shear connection)
  Span type         Composite slabs are designed as one-way slab.
Properties of profiled sheeting  
Use the re-entrant composite floor deck Bondek II    
  Depth of decking hp = mm    
  Characteristic yield strength fyk,p = N/mm2 ; gM0 = 1  
  Design thickness tp = mm    
  Effective area of cross-section Ap = mm2/m    
  Height to neutral axis e = mm    
  Second moment of area of steel core Ip = mm4/m    
  Design value of modulus of elasticity Ep = N/mm2    
  Plastic moment of resistance kNm/m ; gM0 = 1  
  Characteristic resistance to vertical shear kNm/m   assumed
  Design resistance to longitudinal shear N/mm2 ; gVs = 1.25 assumed
    k = N/mm2   assumed
    m= N/mm2   assumed
Properties of materials          
Concrete          
  Concrete grade   Choose the concrete grade
  Type of concrete Normal Weight Concrete    
  Concrete wet density rwc = kg/m3    
  Concrete dry density rc = kg/m3    
  Characteristic value of compressive strength fck= N/mm2    
  Design value of compressive strength N/mm2 ; gC = 1.5  
  Secant modulus of elasticity Ecm= N/mm2    
Reinforcement        
  Characteristic yield strength fyk =    
  Design yield strength   ; gC = 1.5
  Design value of modulus of elasticity Es=    
Slab data        
  Overall slab depth ht=    
  Slab depth above steel decking hc=    
  Effective depth dp = ht - e =      
  Volumn of concrete vc =      
             


Loading per unit area of composite slab-Bondek II
Type of Load Data ULS
composite stage           Partial factors of safety
  Self weight of the sheeting gp = kN/m2 kN/m2 1.35
  Self weight of wet concrete kN/m2 kN/m2 1.35
  Imposed load   kN/m2 kN/m2 1.5
  Total   kN/m2 kN/m2  
Composite stage            
  Self weight of slab kN/m2 kN/m2 1.35
  Floor finishes   kN/m2 kN/m2 1.35
  Imposed load (including partitions and services) q= kN/m2 kN/m2 1.5
  Total   kN/m2 kN/m2  
For deflection of composite slab (frequent combination)            
    kN/m2    
               


Verification of the sheeting as shuttering-Bondek II
1) Simply-spported span
Ultimate limit state
From EN1994-1-1 clause 9.2.3(2), the minimum width of bearing of the sheeting on a steel top flange is 50 mm.
Assuming an effective support at the centre of this width, and a 190 mm steel flange,
the effective length of a simply-supported span is:
  Le= m          
Hence, the design bending moment is:          
  MEd= kNm/m   < Mpl,Rd= kNm/m   ok
Vertical shear:          
  VEd= kN/m   < VRd= kNm/m   ok
Deflection
A note to EN1994-1-1 clause 9.6(2) recommends that the deflection should not exceed span/180.
  d = 5wLe4/(384EaIp) = mm          
The allowable deflection is:          
  mm   < mm   Recalculate
If the deflection is greater than the limit value, recalculate as the continuous slab.      
                 
2) Two-span
Calculate the internal forces
The unpropped sheeting will be verified as a two-span continuous beam resisted uniform loads.
Effective span Le: Le= m          
                 
Case 1                
Max hogging    
     
     
     
     
     
  kN/m2          
  M1a = 0.07031wLe2 = kNm/m          
  MB = -0.125wLe2 = kNm/m          
  VA = VC = 0.375wLe= kN/m          
  VB1 = 0.625wLe= kN/m          
                 
Case 2                
Max sagging            
             
             
             
             
  kN/m2          
  kN/m2          
  M1a = 0.0703w1Le2+0.096w2Le2 = kNm/m          
  MB = -0.125w1Le2-0.06250w2Le2 = kNm/m          
  VA = 0.375w1Le+0.437w2Le = kN/m          
  VB = 0.625w1Le+0.563w2Le = kN/m          
  VC = 0.375w1Le -0.06250w2Le= kN/m          
                 
Internal force                
Maximum sagging bending moment: kNm/m Case 1        
Maximum hogging bending moment: kNm/m Case 2        
Maximum reaction kN/m Case 1        
                 
Design check                
Positive bending: kNm/m   < kNm/m   Recalculate
Negative bending kNm/m   < kNm/m   Recalculate
Support reaction kN/m   < kN/m   Recalculate
                 
All design checks are OK at the ultimate limit state.            
                 
Serviceability limit state
Assume that the section of the sheeting is fully effective. The maximum deflection in span AB, if BC is unloaded and the sheeting is held down at C, is
                 
  mm          
Allowable deflection is:                
  mm   Recalculated        
The serviceability limit state of the construction state is verified.          
                 
2) Three-span
Calculate the internal forces
The unpropped sheeting will be verified as a two-span continuous beam resisted uniform loads.
Effective span Le: Le= m          
                 
Case 1                
             
             
             
             
             
                 
  kN/m2          
  M1 =M3 = 0.08wLe2 = kNm/m          
  MB =Mc= -0.1wLe2 = kNm/m          
  M2 = 0.025wLe2 = kNm/m          
  VA = VD = 0.4wLe= kN/m          
  VB =Vc= 0.6wLe= kN/m          
                 
Case 2                
Max Hogging            
             
             
             
                 
  kN/m2          
  kN/m2          
  M1 = 0.08w1Le2+0.073w2Le2 = kNm/m          
  MB = -0.1w1Le2-0.117w2Le2 = kNm/m          
  VA = 0.4w1Le+0.383w2Le = kN/m          
  VB = 0.6w1Le+0.617w2Le = kN/m          
  VC = 0.5w1Le +0.417w2Le= kN/m          
                 
Case 3                
Max sagging            
             
             
             
             
  kN/m2          
  kN/m2          
  M1 =M3 = 0.08w1Le2+0.101w2Le2 = kNm/m          
  VA = 0.4w1Le+0.45w2Le = kN/m          
  VB = 0.6w1Le+0.55w2Le = kN/m          
                 
Internal force                
Maximum sagging bending moment: kNm/m Case 4        
Maximum hogging bending moment: kNm/m Case 3        
Maximum reaction kN/m Case 3        
                 
Design check                
Positive bending: kNm/m   < kNm/m   Recalculate
Negative bending kNm/m   < kNm/m   Recalculate
Support reaction kN/m   < kN/m   Recalculate
                 
All design checks are OK at the ultimate limit state.
                 


Verification of composite slab-Bondek II
Ultimate limit state  
The design ultimate loading is : w = kN/m2            
Effective span: Le= m            
The continous slab will be designed as a series of simply supported spans.            
The mid-span bending moment is: kNm/m            
The design vertical shear is: kN/m            
                   
1) Bending resistance check
There must be full shear connection, so that the design compressive force in the concrete, Nc,f is :
  kN/m          
The depth of the slab in compression, for full shear connection, is:
  mm <    mm  
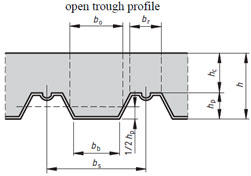
Therefore, the plastic neutral axis is above the sheeting. The distribution of longitudinal bending stresses is shown in Figure 1.
The design resistance to sagging bending is, for full shear connection: Figure 1 Cross-section of composite slab, and stress blocks for sagging bending
  kNm/m <  MEd=   kNm/m Recalculate 
                 
2) Vertical shear resistance check
The recommended value for minimum value (umin) is:
  N/mm2          
in which dp taken as not less than 200. In this problem, dp is taken as 200mm.
The design resistance to vertical shear is:
  kN/m <  VEd=   kN/m Recalculate 
with b is the pitch of deck ribs taken as   mm         For open profiles, their effective width should be taken as the mean width.
b0 is the effective width of the concrete ribs, taken as   mm         For re-entrant profiles, the minimum width should be used.
dp is the depth to the centroidal axis, taken as   mm          
                   
3) Longitudinal shear check  
For longitudinal shear, it is assumed that there is no end anchorage, so that clause 9.7.3 is applicable.  
a) m-k method                
The design shear resistance is:                
  kN/m            
The value used are:                
  b = 1.0 m   dp =   mm    
  Ls = l/4 = 0  mm   Ap =   mm2    
  m =   N/mm2   k =   N/mm2    
This value must not be exceeded by the vertical shear in the slab. Therefor, Vl,Rd is taken as:  
  kN/m < VEd=   kN/m Recalculate If this method is not verified longitudinal shear check, uses partial connection theory
                   
Serviceability limit state  
Control of cracking of concrete  
As the slab is designed as simply supported, only anti-crack reinforcement is needed. The cross-sectional area of the reinforcement above the ribs should be not less than 0.2% for un-propped construction.  
  min As = 0.002 x b x hc = mm2/m            
and the A252 mesh used here is sufficient. with As = 252 mm2/m (f8 a200)          
                   
Deflection  
Second moment of area  
The short-term elastic moduli and modular ratios are:  
               
For buildings, EN 1994 permits the simplification that all strains may be assumed to be twice their short-term value.  
The long-term elastic moduli and modular ratios are:  
               
The depth of neutral axis (counted from the top of slab) is then given by the 'first moments of area' equation: See R.P.JOHNSON's books
                 
Hence mm            
The second moment of area is:  
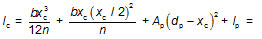  mm4/m            
The total load is taken as, using the frequent combination for calculating the deflection of composite slab:  
  kN/m2            
                   
For the calculation of delecftion, firstly, the slab is considered to be simply supprted.  
The mid-span deflection is:               If the deflection is greater than the limit value, recalculate as the continuous slab.
  mm            
The allowable deflection is:               A more accurate calculation for the continuous slab, assuming 15% of each span to be cracked
  mm <   mm Recalculate  
                   
All design checks are OK at both the ultimate limit state and the serviceability limit state.  
                   
Back to Top